Understanding Quantum Mechanics IV: What Are Photons?

A simple model for photons answering Einstein's wish

Planck discovered the quantum of action ℏ while studying light. He discovered that he could describe the colour of hot objects only if he assumed that light consisted of light quanta or photons. Many experiments confirmed their existence. Einstein gave some convincing arguments for their existence.

Towards the end of his life, Einstein wrote:

Fünfzig Jahre intensiven Nachdenkens haben mich der Antwort auf die Frage: „Was sind Lichtquanten?“ nicht näher gebracht. Natürlich bildet sich heute jeder Wicht ein, er wisse die Antwort. Doch da täuscht er sich.

Translated:

50 years of intense thinking have not brought me closer to the answer to the question: what are light quanta? Of course, today everybody thinks he has the answer. But he is wrong.

Any model for photons is required explain at least the following observations:

• The invariant speed of photons, thus their lack of mass,

• The spin, boson character, and all its other quantum numbers,

• Its relation to U(1) gauge symmetry,

• The relation for photon energy E=ℏ 𝜔 and for its momentum p = 2𝜋 ℏ / 𝜆,

• The possibility of observations and measurements,

• The two-slit experiment,

• The relation of photons to charge and to Maxwell’s equations.

Here is a photon model that fulfills the requirements, and in particular, realizes wave-particle duality and the relation between crossing switches and ℏ. Recall that strands are unobservable, while their crossing switches are.

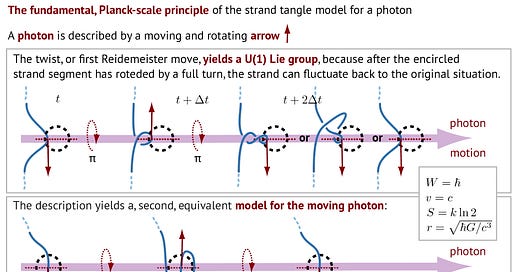
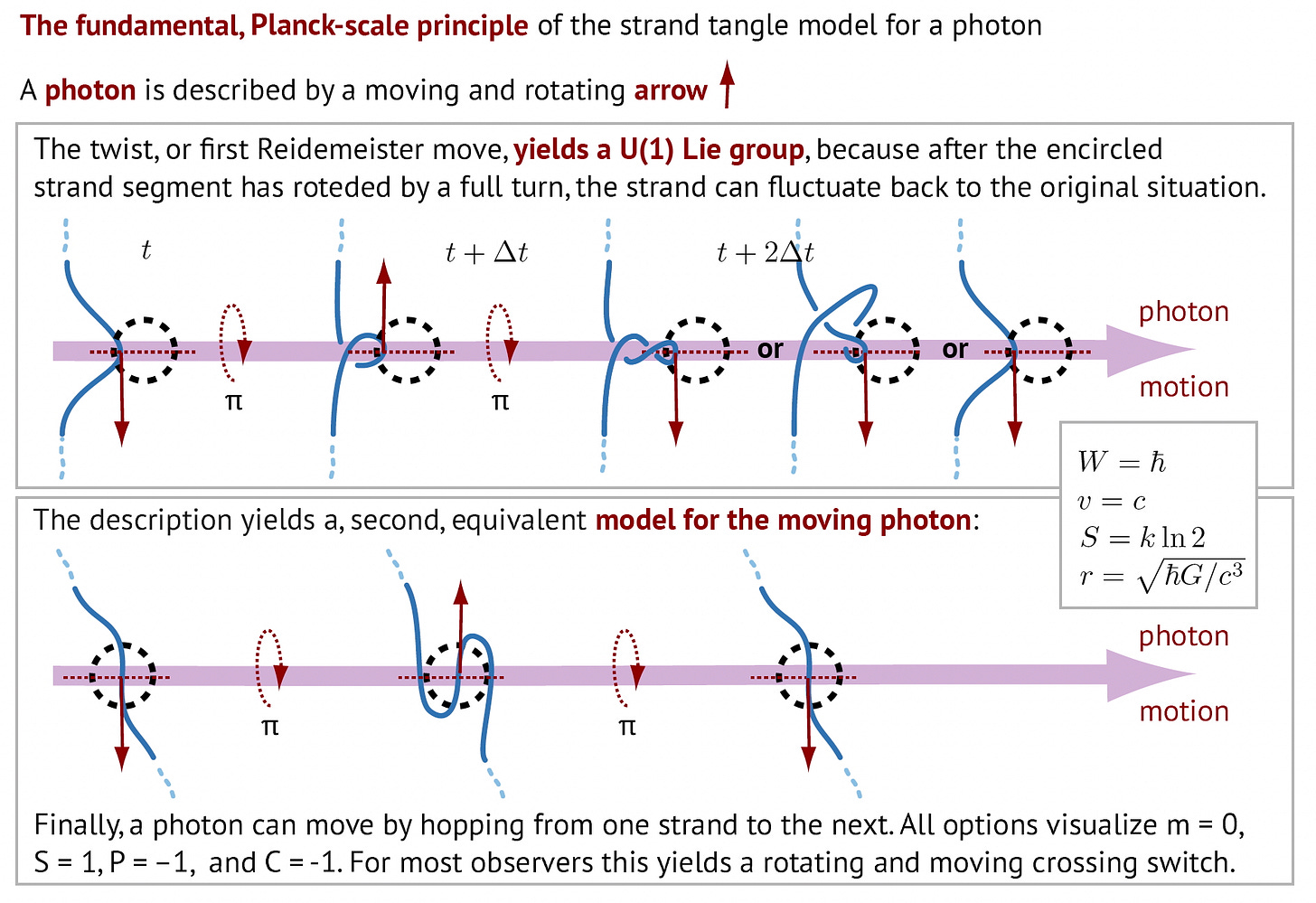
We can imagine the photon moving towards the right, and the loop rotating around the direction of motion, like an advancing screw or a propeller with one wing. The length of the loop is the wavelength. The radius of the strand is the Planck length: the strand itself is thus not observable, because nothing that small is observable. The figure shows that every rotation of the loop leads to a crossing switch. The two photon helicities appear naturally. Spin 1 - returning to the original state after a rotation by 2𝜋 - is also realized. (This way to describe a photons is similar to the “schmoton” model that is found on the internet - but the schmoton model fails to explain and include the quantum of action ℏ.)

Above all, the figure shows that photons follow de Broglie’s relation for wavelength and momentum. No other model for photons does so. The quantum of action ℏ arises in de Broglie’s relation because every crossing switch produces ℏ.

The photon model also implies spin 1 and U(1). The geometry implies the quantum numbers of the photon and their boson character: twists can jump from a strand to the next, which yields boson character. All models imply that photons advance like screws, but also imply the lack of masse for the photon: mass arises if a chiral tangle requires Dirac’s trick to rotate. Photons do not require it for their rotation.

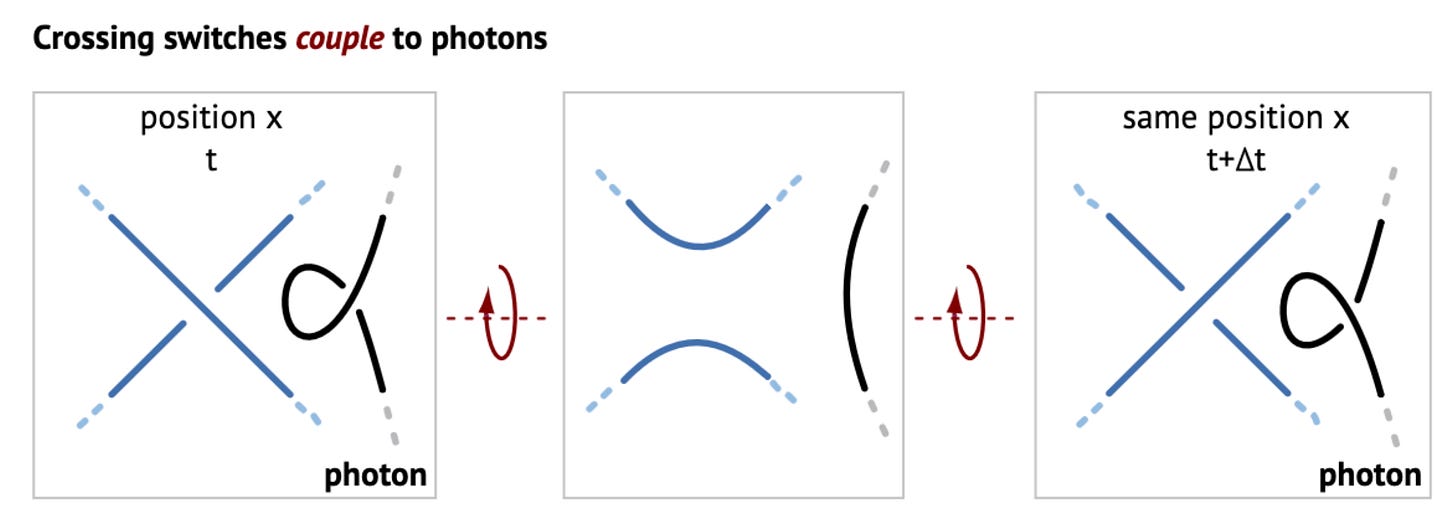
The photon model also explains that all observations are electromagnetic. All observations require the quantum of action ℏ. This is shown in this image:

This image explains why crossing switches couple to photons, and thus why crossing switches are observable while strands themselves are not. (The image also shows why quantum theory minimizes action, i.e., minimized the number of crossing switches.)

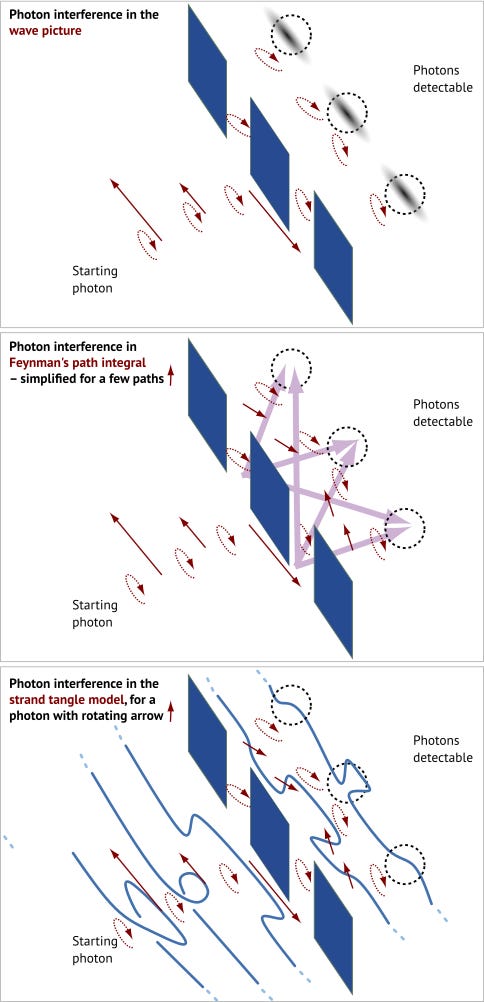
The strand model of photons also explains the two-slit experiment:

The addition region is the region with untangled strands that connects the partial photons. (Additions regions describe quantum superpositions, as told in the text linked at the end.) Strands confirm, as Dirac noted, a photon only interferes with itself. One notes that the strand explanation requires that the motion of photons can occur by hopping from a strand to a neighbouring one.

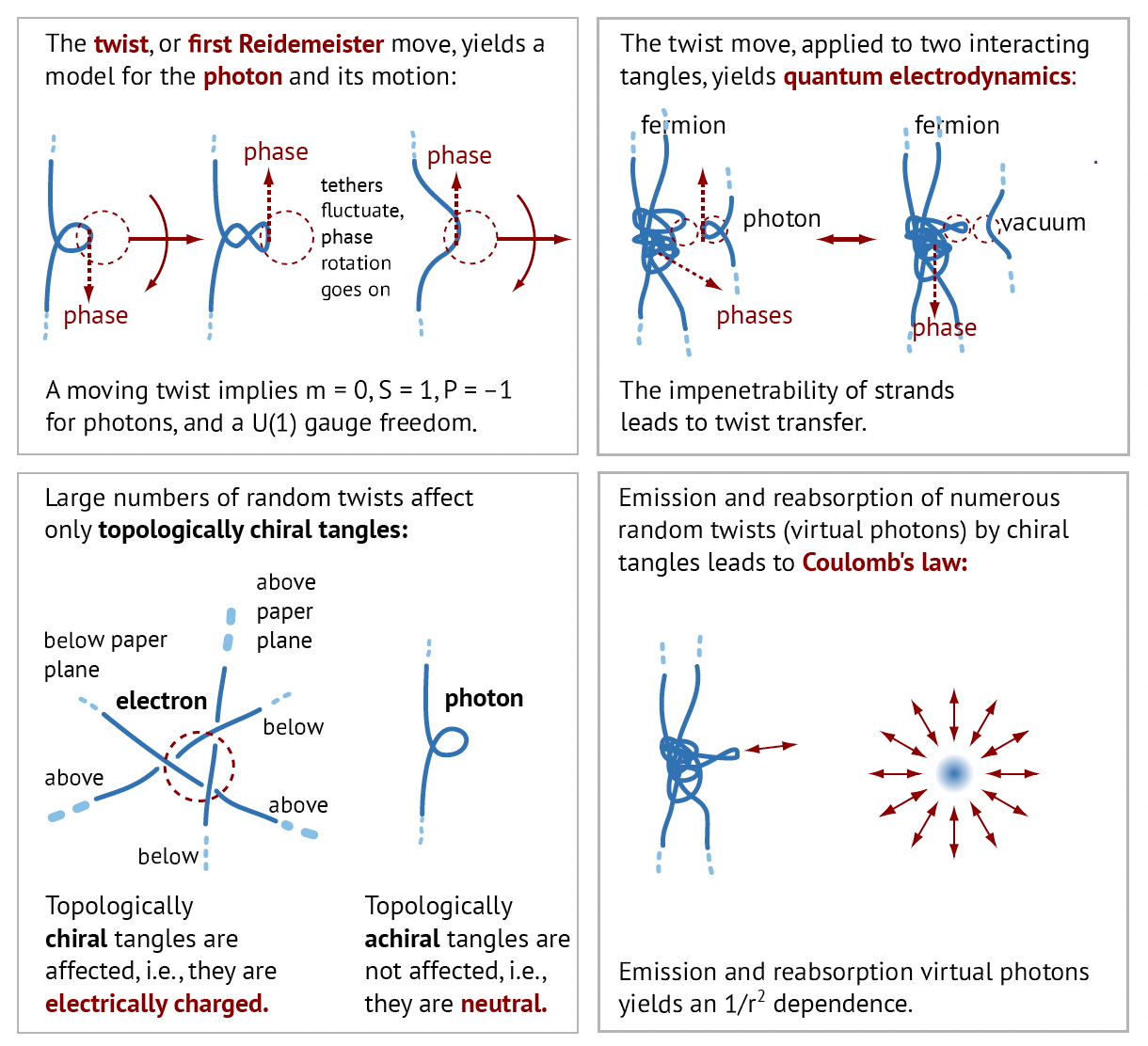
The last requirement for a photon model is to deduce classical electrodynamics. A graphical summary is here:

In simple terms, electric charge is due to the topological chirality of tangles. Charge emits and absorbs photons. Charge, being due to topology, is conserved. Coulomb’s law holds. As a result of the last two properties, Maxwell’s equations, arise from large numbers of such photons.

In other words, describing each photon as an unobservable strand with a rotating loop reproduces everything we know about light. Above all, this explains both the wave and the particle aspects of photons. The text linked here is a bit long, but tells the story in more detail. (It also tells the story for all other elementary particles.) In particular, the text tells how to visualize quantum theory for matter particles, for photons, and for all other radiation particles. Enjoy.

*