From strands to de Broglie's relation

Why ℏ arises in quantum waves - Understanding quantum mechanics III

Quantum mechanics started with the discovery of Planck’s quantum of action ℏ, continued with de Broglie’s relations and then was complete with the various evolution equations for the wave functions, from Schrödinger’s equation to Dirac’s equation.

So why does de Broglie’s relation work? Why does ℏ appear in the expression of the momentum of a quantum particle? This is the first question to be answered by any model that claims to deduce quantum mechanics.

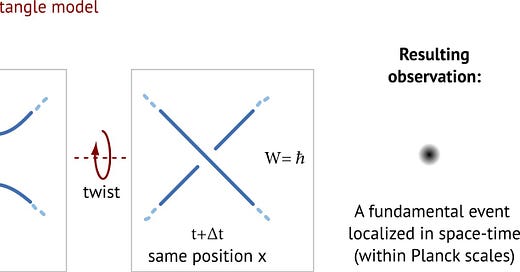
The strand model deduces all physical laws from the fundamental principle. It states: Planck’s quantum of action ℏ is due to observable crossing switches of unobservable strands. The figure explains what is meant:

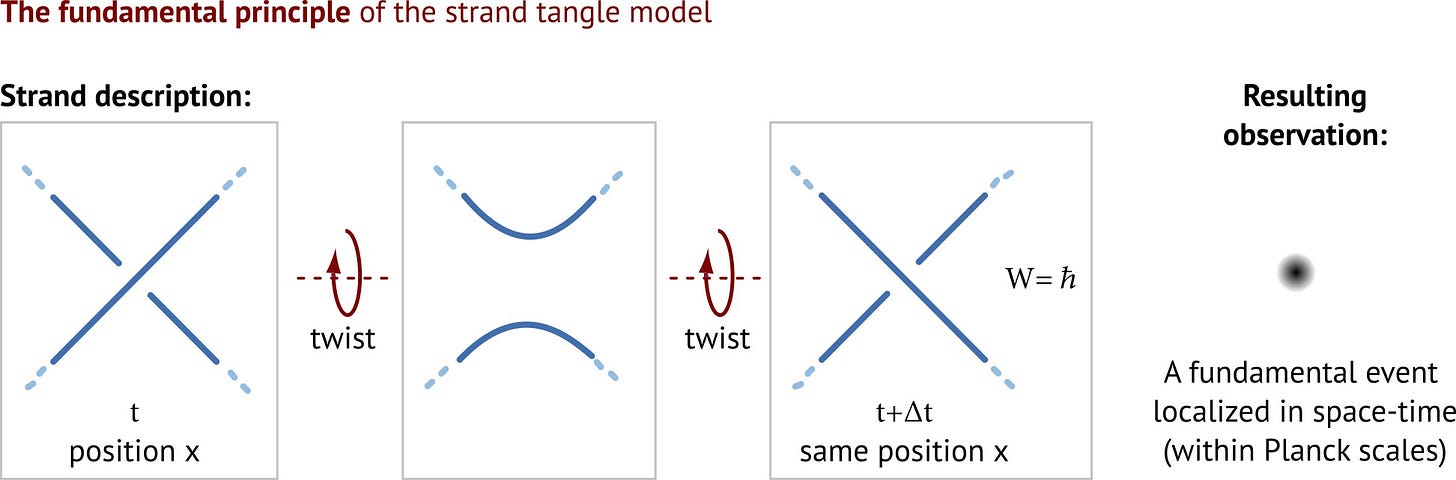
It does take only a few steps to deduce de Broglie’s relation from the fundamental rpinciple. First, we recall that particles are rotating tangles. When their tangled core rotates , i.e., when the particle spins, the crossings generate the wave function:

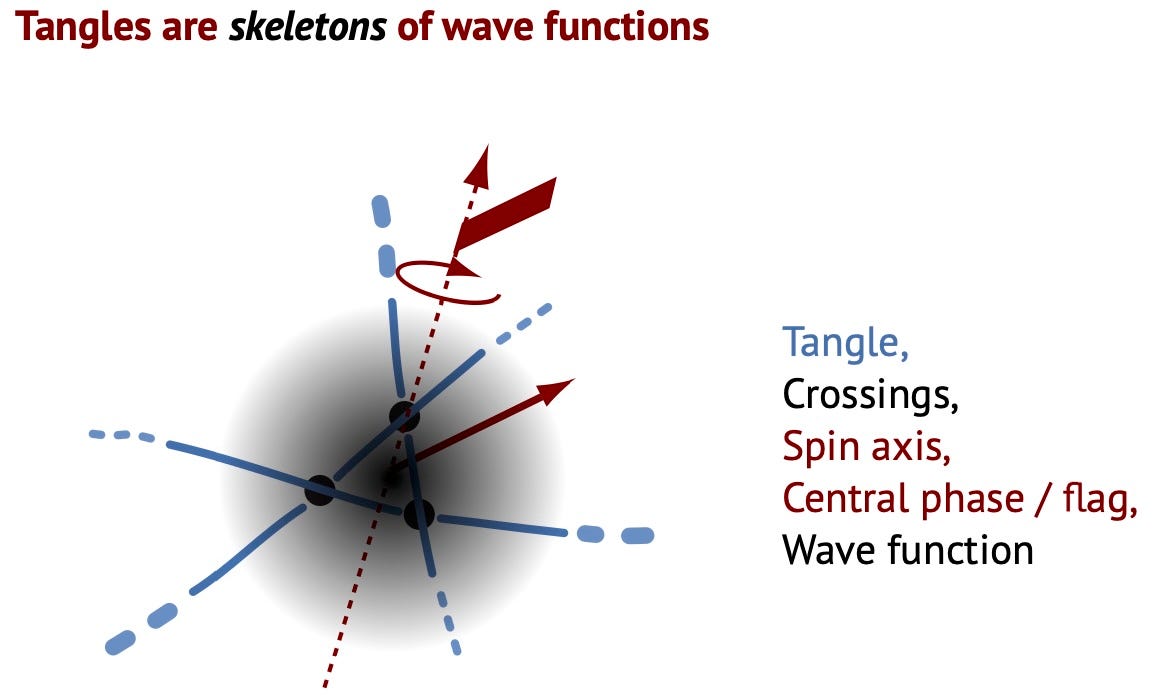
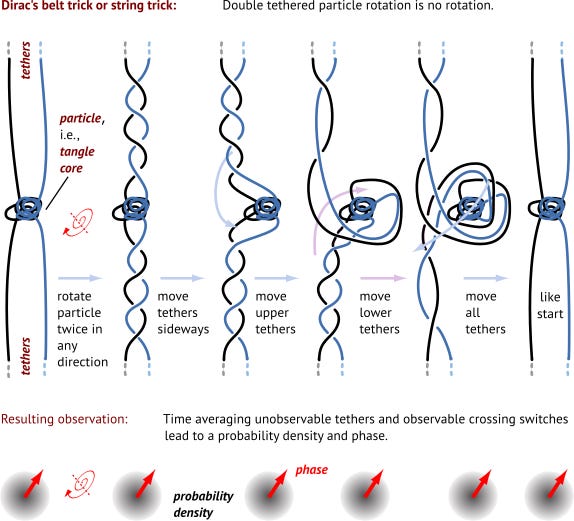
And now comes the interesting part. When such a tangle rotates, or spins, its strands tangle up and untangle again, all the time, using Dirac’s trick and the inherent fluctuations:

The difference to the grphic is that electrons and the other leptons consist of three strands, not two. But Dirac’s trick remains the same.

Now, every Dirac trick correponds to a crossing switch (a few, to be precise). Therefore, a moving and spinning particle produces crossing switches along its path.

Now, each crossing switch produces ℏ. When a particle moves, it produces crossing switches along its path. In nature, momentum is defined as action W per length l. Therefore, momentum is defined as the number of crossing switches per length: p= W/l. A particle thus moves in vacuum like a maple seed falls though air: it advances like a small propeller. The main difference between a maple seed or propeller and a particle is that the particle is tethered, so that, on average, a Dirac trick is needed for every (second) rotation.

But this periodic Dirac trick of the spinning tangle, which produces an ℏ at every turn, and thus at every wavelength 𝝀, is the reason that ℏ appears in de Broglie’s relation p=ℏ/𝝀. An the chirality of the propeller, oops, of the particle, determines the mass value. Indeed it does, as we will see later on.

Now you might say that this does explain de Broglie’s relation for electrons. But Planck discovered ℏ in photons, not in electrons, and the relation applies to photons as well. How does that happen? This will be explained in the next episode. And ℏ also appears in other situations. Inded - and all the situations can be explained with crossing switches of strands.

*