A colleague, a great scientist, and I are writing everything known about quantum mechanics in an intuitive and complete way. We have a simple aim: we want to make easy and intuitive what is difficult about quantum mechanics.
Quantum mechanics is the exploration of wave-particle duality. The observations in this domain of nature can be summarized in this way:
Quantum particles are observed to be point-like, to be fermions or bosons, to have spin, and to be countable. Quantum particles also behave as (quantum) waves. These waves are observed to be extended, to interfere, and to be probabilistic.
At school, we learn de Broglies’s relation, about wave functions, and maybe a bit about their evolution. We are told that wave functions for fermions describe extension, but, alas, they do not describe countable particles. We learn that photons are bosons and have no wave functions. We learn that spin or helicity are hard to visualize using wave functions. In other words, thinking in wave functions only captures a part of wave-particle duality, and thus only captures a part of all quantum effects. In particular, wave functions do not explain Planck’s quantum of action. Let us put it more directly: wave functions make quantum theory hard to grasp.
To imagine and understand quantum theory requires a visualization that captures both extended wave functions and countable particles with spin. Interestingly, there is such a visualization. Its origin is buried in the literature and starts in 1929, with Dirac. Let me start with a summary. The details follow afterwards.
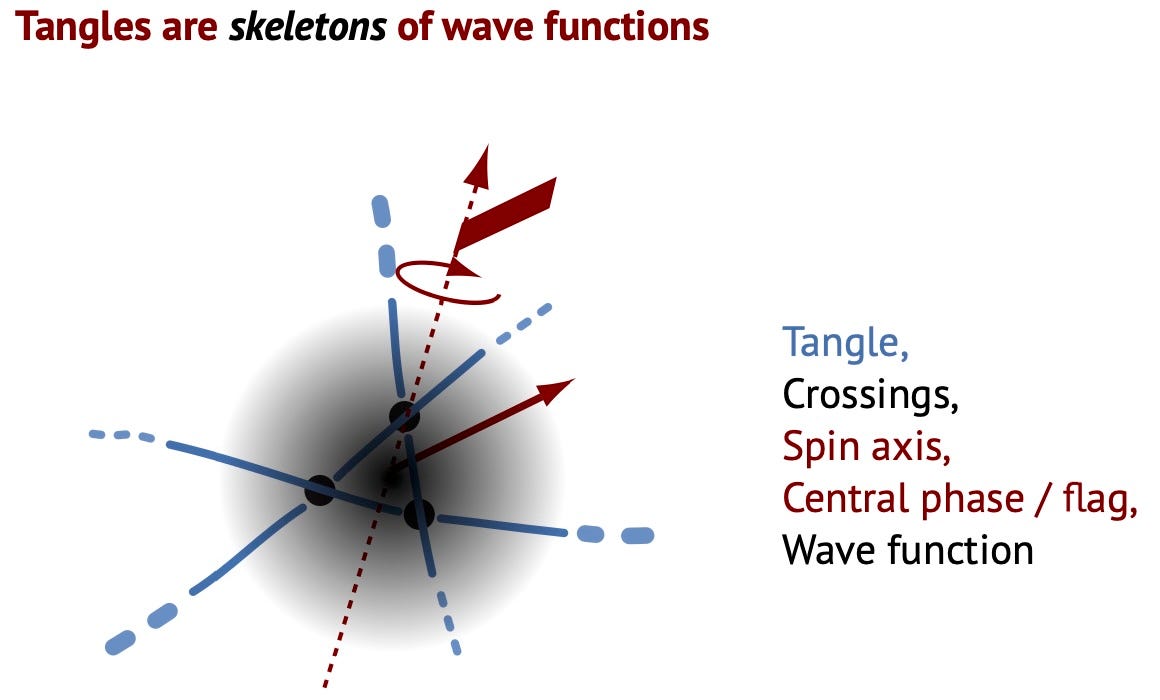
A quantum particle is a rotating (rational 3d) tangle of unobservable strands whose crossing switches are observable and define Planck’s quantum of action.
The wave function is the oriented crossing density of a fermion tangle. Spin is due to the rotation of the tangles. Photons are trivial tangles, fermions are non-trivial tangles.
The position of a particle is the position of its tangled region - its tangle core. The wave properties are due to the extension of tangle cores. Particles are countable because cores are countable. Spin arises because cores can rotate.
Let me go through the model step by step. The next picture captures the basic idea about particles and their wave functions:
A (continuously fluctuating) rational 3d tangle, shown in blue, describes a single particle. The strands are fluctuating in shape all the time. Because the tangle is non-trivial, it describes a fermion. Because it has three strands, it is a lepton. Because of its topology, it is an electron. All this will be explained in future blog entries.
The tangle rotates all the time. Here is an animation of the rotating tangle of an electron, without any shape fluctuations:
The original is even more beautiful and is found at https://www.desmos.com/3d/sgoubdnuys. It was produced by ronwnor.
I will convince you in the following that this model describes everything about quantum theory and everything about the electron that is known. For example, each of the three central crossings yields 1/3 of an elementary charge. The rotation is the electron spin. The connections to spatial infinity yield fermion and spin 1/2 behaviour. A mirror tangle rotating in opposite dorection is a positron. The oriented crossing density is the wave function. The orientation of the central triangle is the phase. The position of the central triangle is the position of the electron. Also the mass value of the electron can be estimated, as shown later on. The crossing switches per rotation yield de Broglie’s relations, wave particle duality, and the Schrödinger equation. But also Dirac’s equation. And a model for photons and for all other particles arises. And much more. You will enjoy this adventure.
*
Above all, the strands are unobservable, because the strands have Planck radius. And nothing that has the size of a Planck length is observable. But the rotating tangled region produces crossing switches, as will be shown soon, and these, in full contrast, are observable. The density of crossing switches yields the probability density of the wave function.
The motion shown in the animation is called Dirac’s trick. The size of the region used for Dirac’s trick is the extension of the wave function, and thus yields the wave aspect of the electron. First of all, enjoy the exploration by yourself. Then read further.
*
In nature, the shape of the strands is continuously fluctuating. Wave functions are blurred tangles. Conversely, tangles are fluctuating skeletons of wave functions. Recalling these two statements will make quantum theory intuitive.
First of all, tangles can be counted. Each tangle is a particle. The animation above proves that the tangle shown – a non-trivial rational 3d tangle – has spin 1/2: it returns to itself after a double rotation.
Tangles with the same topology represent identical particles. Non-trivial tangles are fermions. This can be seen with the following animation, made by Antonio Martos, which uses belts instead of tangles. Just imagine that each edge of the belt is a strand. (If you can produce an animation with tangles, let me know …)
In other words, non-trivial tangles reproduce spin 1/2 behaviour and fermion behaviour - as long as we recall that the strands are unobservable, and that only the tangled region is somehow observable. This will be explained in the next entry.
*
P.S.: If you want to read more about this visualization without waiting for the next blog entry, have a look at this text, entitled Testing a model for emergent spinor wave functions explaining elementary particles and gauge interactions.
P.P.S.: A general introduction with detailed explanations and publications about the strand tangle model is found here. The model goes far beyond quantum mechanics.