Understanding quantum mechanics - II

The role of Planck's quantum of action

The previous text recalled how Dirac, in 1929, explained spin 1/2, or, more precisely, spin ℏ/2 using tethers.

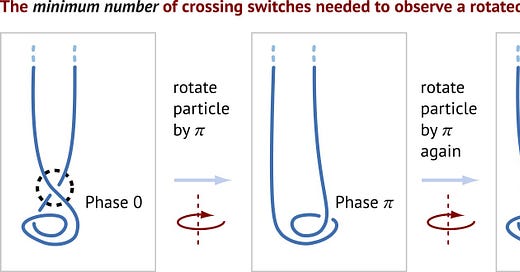
But Dirac trick does much more. Imagine a ball hanging with two parallel strands from an infinitely distant ceiling. Now you rotate the ball by -𝜋. The you unwind and come back and rotate it by +𝜋, and compare it with the situation at -𝜋. The difference is the sign of the crossing, a so-called crossing switch:

Now, angular momentum is action per rotation. There is one full rotation between the left and the right image. Thus one crossing switch is Planck's quantum of action ℏ.

This was already stated in this way by Lou Kauffman in 1987.

This fundamental principle defines Planck’s quantum of action ℏ. (One can see this figure as a (rotated) cut-out of the previous one.)

It turns out that all quntum effects in nature, thus all effects in which ℏ appears, are due to crossing switches. And vice versa, all crossing switches lead to quantum effects.

The strands have Planck radius, and are unobservable. Only their crossing switches are observable.

For example, de Broglie’s relations follow from crossing switches. So do Heisenberg’s uncertainty relation, Heisenberg’s canonical commutation relation, the Schrödinger relation, and the Dirac equation.

Also particles and wave functions follow from crossing switches. Particles are tangles of strands. Spinning particles are spinning tangles. This yields a wave function amplitude and phase. The next figure shows the details.

It turns out that this definition of wave function produces fermion behaviour, spin, the exclusion principle, intereference, the Stern-Gerlach experiment, Hilbert spaces, photons, the path integral formulation, and all other effects and aspects of quantum theory.

But most interestingly, this definition allows us to visualize quantum theory. In short, we can understand quantum theory using strands.

An older presentation is found here. A new paper on this topic, from which the figures are taken, will appear soon.

Is understanding enough? No. The exploration will show not only that we can understand quantum theory in this way. Strands allow us to understand things that are not understood so far - from the measurement problem to relativistic quantum gravity, the masses of elementary particles and more.

This post was only about the derivation of the model for Planck’s quantum of action ℏ. In simple terms, ℏ has a topological (and geometric) origin. More details will follow. In the meantime, you might be interested to work out for yourself how this definition leads to your favorite quantum effect.

*