What is a wave function?
MotionMountain - Physics For Others
Experiments show that each quantum particle is described by a wave function. The square of the wave function is the probability density, i.e., the probability to find the particle at a given spot.
We are used to think of the wave function as a cloud with a direction: the direction is called the phase of the wave function, the denisty of the cloud is the square root of the probability density (I simplify somewhat).
Everybody thinks that this is too abstract. Well, here is a simple way to think about the wave function more concretely:
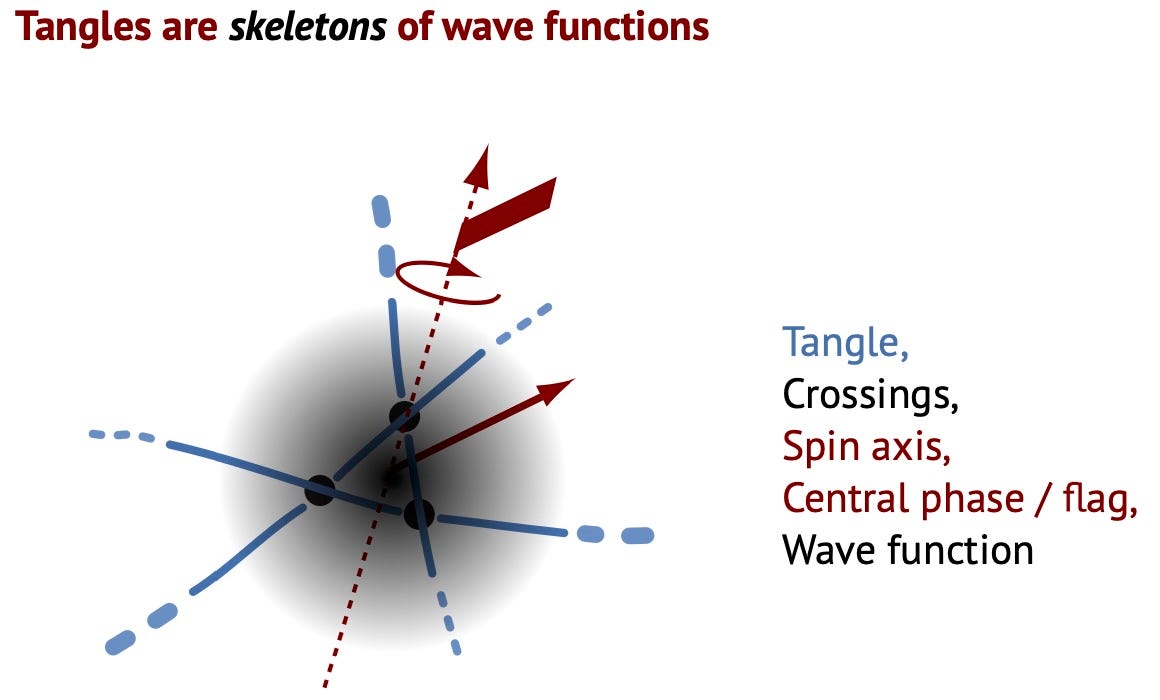
Wave functions are crossing densities of fluctuating tangles of strands. Conversely, tangles are skeletons of wave function. This requires to take into account that strands are invisible. Only their crossings from the wavefunction.
It turns out that this approach implies all of quantum theory. I told this in this pedagogical text: researchgate.net/publication/361866270
Since this is my first post on substack, I’ll keep the story short. It turns out that this approach implies all of quantum theory. In fact, it allows visualizing quantum theory. For example, the approach explains Hilbert spaces, visualizes uncertainty, implies non-commutativity and describes entanglement.
In other words, this trick about how to image wave functions allows us to understand quantum theory. I will tell more in the near future.
There is no "wave function of the universe". Wave functions are for physical systems that can be observed from the outside. This is not the case for the universe.
In case of Universe (free field) equations where number of particles are not constant use of wave function is limited. Still, same equations satisfy for non interaction cases and we reach on some ideal solution. When wave functions used for non relativistic particles in isolated quantum states then probability of true results itself becomes high.